J. Bethencourt, A. Sahai and B. Waters, “Ciphertext-Policy Attribute-Based Encryption,” 2007 IEEE Symposium on Security and Privacy (SP '07), 2007, pp. 321-334, doi: 10.1109/SP.2007.11.
python的charm-crypto库,abenc_bsw07源码阅读
CP-ABE方案首次由 J. Bethencourt,A. Sahai 和 B. Waters在 IEEE Symposium on Security and Privacy (SP '07)上发布,该方案也常被成为BSW(三人名字首字母)。该方案改善了Sahai等人在2005年发表的基于身份的模糊加密方案 (FIBE),该方案将用户身份分解成一系列描述用户身份的属性,加密者加密数据时指定一个属性集合和阈值d ,解密者必须拥有至少d个给定的属性才能正确解密密文。FIBE方案是BSW方案的雏形。因为BSW方案是对FIBE方案的改进,在算法设计中也使用了FIBE方案的思想和运算原理,在其基础上添加了访问控制树,以及递归求解访问控制树 。
1.方案定义
该方案由5个基本算法组成:Setup、Encrypt、KeyGen、Decrypt和 Delegate。
S e t u p \mathrm{Setup} Setup E n c r y p t ( P K , M , A ) → C T \mathrm{Encrypt}(PK, M, A) → CT Encrypt ( P K , M , A ) → CT K e y G e n ( M K , P K , S ) → S K \mathrm{KeyGen}(MK, PK, S)→ SK KeyGen ( M K , P K , S ) → S K D e c r y p t ( P K , C T , S K ) → M \mathrm{Decrypt}(PK, CT, SK) → M Decrypt ( P K , CT , S K ) → M D e l e g a t e ( S K , S ~ ) → S K ~ \mathrm{Delegate}(SK,\tilde{S})\to \tilde{SK} Delegate ( S K , S ~ ) → S K ~ S S S S K SK S K S ~ \tilde{S} S ~ S ~ ⊆ S \tilde{S}\subseteq S S ~ ⊆ S S ~ \tilde{S} S ~ S K ~ \tilde{SK} S K ~
2.算法详细设计
该方案用到以下基本条件:
令G 0 G_0 G 0 p p p g g g G 0 G_0 G 0
令e : G 0 × G 0 → G 1 e:G_0\times G_0\to G_1 e : G 0 × G 0 → G 1
群的大小由安全参数λ \lambda λ
对于i ∈ Z p i\in Z_{p} i ∈ Z p Z p Z_p Z p S S S Δ i , S ( x ) = ∏ j ∈ S , j ≠ i x − j i − j \Delta_{i,S}(x)=\prod_{j\in S,j\neq i}\frac{x-j}{i-j} Δ i , S ( x ) = ∏ j ∈ S , j = i i − j x − j
应用一个哈希函数H : { 0 , 1 } ∗ → G 0 H:\{0,1\}^*\to G_0 H : { 0 , 1 } ∗ → G 0
2.1 Setup
该算法以隐含安全参数λ \lambda λ
该算法选择一个阶为p p p G 0 G_0 G 0 g g g α , β ∈ Z P \alpha,\beta \in Z_P α , β ∈ Z P P K = ( G 0 , g , h = g β , f = g 1 β , e ( g , g ) α ) PK=(G_0,g,h=g^\beta,f=g^{\frac1\beta},e(g,g)^\alpha) P K = ( G 0 , g , h = g β , f = g β 1 , e ( g , g ) α ) M K = ( β , g α ) MK=(\beta,g^\alpha) M K = ( β , g α )
2.2 KeyGen
K e y G e n ( M K , P K , S ) → S K \mathrm{KeyGen}(MK, PK, S)→ SK KeyGen ( M K , P K , S ) → S K M K MK M K S S S S K SK S K
首先随机选择一个随机数r ∈ Z p r\in Z_{p} r ∈ Z p j ∈ S j\in S j ∈ S r j ∈ Z p r_j\in Z_p r j ∈ Z p S S S Z p Z_p Z p r j r_j r j
S K = ( D = g α + r β , ∀ j ∈ S : D j = g r ⋅ H ( j ) r j , D j ′ = g r j ) SK=(D=g^{\frac{\alpha+r}\beta},\forall j\in S:D_j=g^r\cdot H(j)^{r_j},D_j^{^{\prime}}=g^{r_j})
S K = ( D = g β α + r , ∀ j ∈ S : D j = g r ⋅ H ( j ) r j , D j ′ = g r j )
利用P K PK P K M K MK M K S S S
∀ j ∈ S : D j = g r ⋅ H ( j ) r j , D j ′ = g r j \forall j\in S:D_j=g^r\cdot H(j)^{r_j},D_j^{'}=g^{r_j} ∀ j ∈ S : D j = g r ⋅ H ( j ) r j , D j ′ = g r j S S S Z p Z_p Z p D j D_j D j D j ′ D_j^{^{\prime}} D j ′
2.3 Encrypt
E n c r y p t ( P K , M , A ) → C T \mathrm{Encrypt}(PK, M, A) → CT Encrypt ( P K , M , A ) → CT P K PK P K M M M A A A M M M C T CT CT A A A C T CT CT
首先对访问结构A A A T T T x x x q x q_x q x R R R x x x q x q_x q x d x d_x d x x x x k x k_x k x d x = k x − 1 d_x=k_x-1 d x = k x − 1
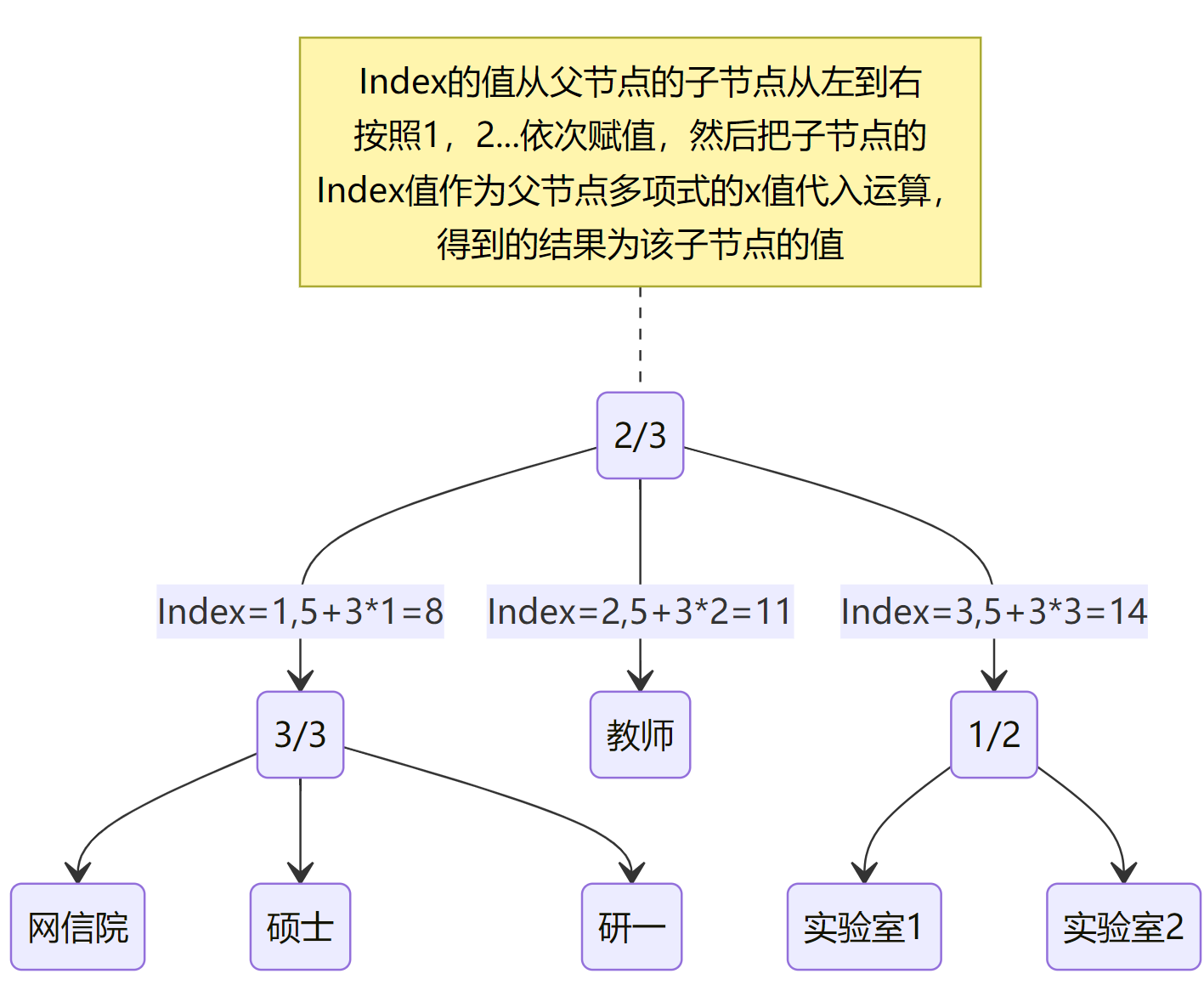
从根节点R R R s ∈ Z p s\in Z_{p} s ∈ Z p q R ( 0 ) = s q_R(0)=s q R ( 0 ) = s q R q_R q R d R d_R d R x x x q x ( 0 ) = q p a r e n t ( x ) ( i n d e x ( x ) ) q_x(0)=q_{parent(x)}(index(x)) q x ( 0 ) = q p a re n t ( x ) ( in d e x ( x )) q x q_x q x d x d_x d x
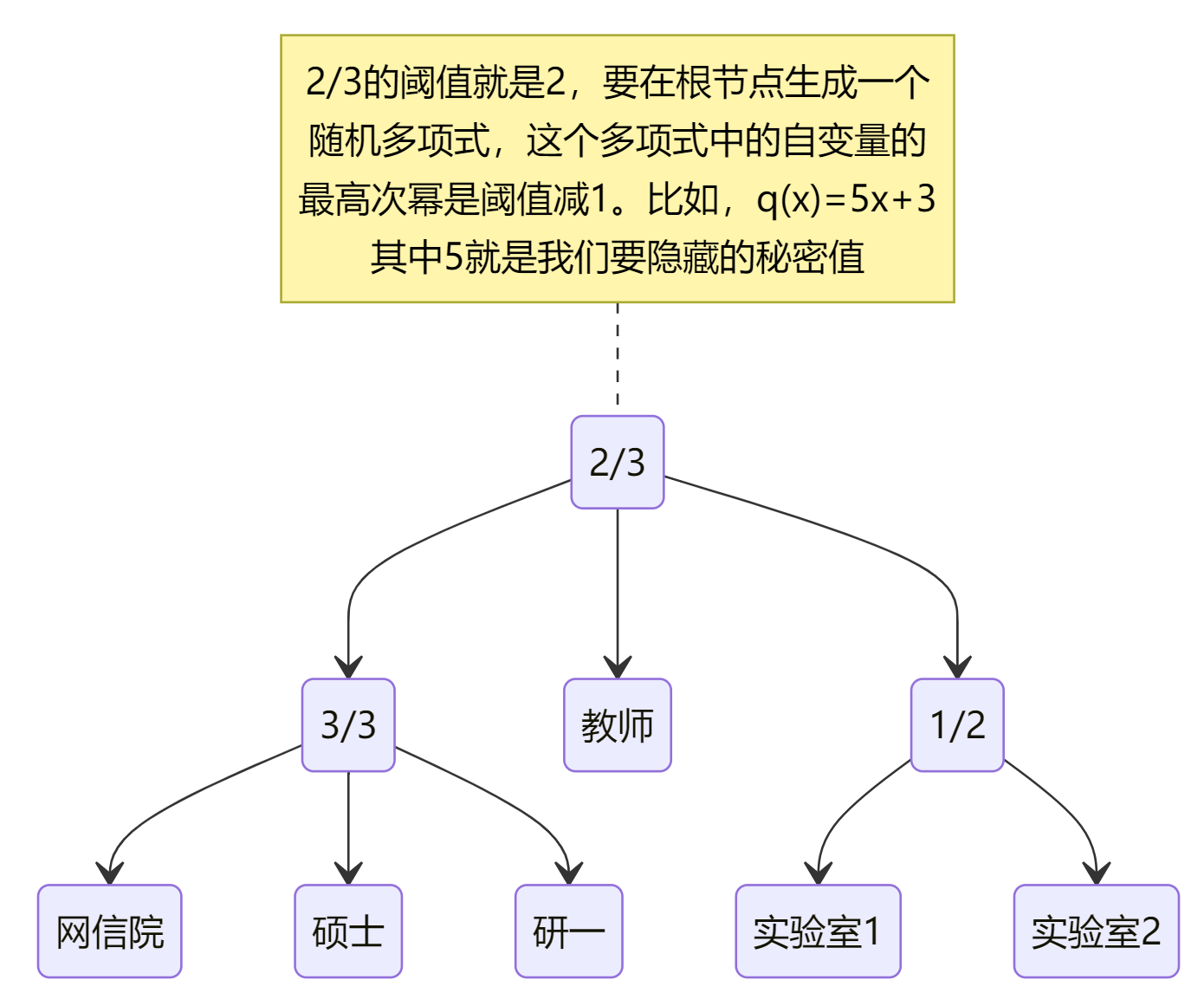
有点费解,那就举个例子吧!
由图可知,属性值都在叶子节点上,而非叶子节点都是满足条件个数的门限。除了叶子节点,所有非叶子节点都是a / b a/b a / b b b b a a a q x q_x q x q x q_x q x k x k_x k x a / b a/b a / b a a a
接下来,对这一层的非叶子节点再按照根节点的多项式生成规则,为其随机生成多项式。
令Y Y Y T T T
C T = ( T , C ~ = M e ( g , g ) α s , C = h s , ∀ y ∈ Y : C y = g q y ( 0 ) , C y ′ = H ( a t t ( y ) ) q y ( 0 ) ) CT=(T,\tilde{C}=Me(g,g)^{\alpha s},C=h^s,\forall y\in Y:C_y=g^{q_y(0)},C_y^{\prime}=H(att(y))^{q_y(0)})
CT = ( T , C ~ = M e ( g , g ) α s , C = h s , ∀ y ∈ Y : C y = g q y ( 0 ) , C y ′ = H ( a tt ( y ) ) q y ( 0 ) )
T T T
C ~ = M e ( g , g ) α s \tilde{C}=Me(g,g)^{\alpha s} C ~ = M e ( g , g ) α s M M M s s s Z p Z_p Z p
C = h s C=h^s C = h s
∀ y ∈ Y : C y = g q y ( 0 ) , C y ′ = H ( a t t ( y ) ) q y ( 0 ) \forall y\in Y:C_y=g^{q_y(0)},C_y^{\prime}=H(att(y))^{q_y(0)} ∀ y ∈ Y : C y = g q y ( 0 ) , C y ′ = H ( a tt ( y ) ) q y ( 0 )
2.4 Decrypt
D e c r y p t ( P K , C T , S K ) → M \mathrm{Decrypt}(PK, CT, SK) → M Decrypt ( P K , CT , S K ) → M
解密过程是一个递归算法D e c r y p t N o d e ( C T , S K , x ) \mathrm{DecryptNode}(CT,SK,x) DecryptNode ( CT , S K , x ) C T = ( T , C ~ , C , ∀ y ∈ Y : C y , C y ′ ) CT=(T,\tilde{C},C,\forall y\in Y:C_y,C_y^{^{\prime}}) CT = ( T , C ~ , C , ∀ y ∈ Y : C y , C y ′ ) S S S S K SK S K T T T x x x
假如x x x i = a t t ( x ) i=att(x) i = a tt ( x ) i ∈ S i\in S i ∈ S
D e c r y p t N o d e ( C T , S K , x ) = e ( D i , C x ) e ( D i ′ , C x ′ ) = e ( g r ⋅ H ( i ) r i , h q x ( 0 ) ) e ( g r i , H ( i ) q x ( 0 ) ) = e ( g , g ) r ⋅ q x ( 0 ) \mathrm{DecryptNode}(CT,SK,x)=\frac{e(D_i,C_x)}{e(D_i^{'},C_x^{'})}=\frac{e(g^r\cdot H(i)^{r_i},h^{q_x(0)})}{e(g^{r_i},H(i)^{q_x(0)})}=e(g,g)^{r\cdot q_x(0)}
DecryptNode ( CT , S K , x ) = e ( D i ′ , C x ′ ) e ( D i , C x ) = e ( g r i , H ( i ) q x ( 0 ) ) e ( g r ⋅ H ( i ) r i , h q x ( 0 ) ) = e ( g , g ) r ⋅ q x ( 0 )
这个过程需要用到双线性映射的性质。
如果i ∉ S i\notin S i ∈ / S
现在考虑非叶子节点时的递归情况,当x x x x x x z z z D e c r y p t N o d e ( C T , S K , z ) \mathrm{DecryptNode}(CT,SK,z) DecryptNode ( CT , S K , z ) F z F_z F z S x S_x S x k x k_x k x z z z
F x = ∏ z ∈ S x F z A i , S x ( 0 ) = ∏ z ∈ S x ( e ( g , g ) r ⋅ q p a r e n t ( z ) ( i n d e x ( z ) ) ) A i , S x ′ ( 0 ) = ∏ z ∈ S x e ( g , g ) r ⋅ q x ( i ) ⋅ A i , S x ′ ( 0 ) = e ( g , g ) r ⋅ q x ( 0 ) \begin{aligned}F_x&=\prod_{z\in S_x}F_z^{A_{i,S_x}(0)}=\prod_{z\in S_x}\left(e(g,g)^{r\cdot q_{parent(z)}(index(z))}\right)^{A_{i,S_x^{\prime}}(0)}\\&=\prod_{z\in S_x}e(g,g)^{r\cdot q_x(i)\cdot A_{i,S_x^{\prime}}(0)}=e(g,g)^{r\cdot q_x(0)}\end{aligned}
F x = z ∈ S x ∏ F z A i , S x ( 0 ) = z ∈ S x ∏ ( e ( g , g ) r ⋅ q p a re n t ( z ) ( in d e x ( z )) ) A i , S x ′ ( 0 ) = z ∈ S x ∏ e ( g , g ) r ⋅ q x ( i ) ⋅ A i , S x ′ ( 0 ) = e ( g , g ) r ⋅ q x ( 0 )
其中,i = i n d e x ( z ) i=index(z) i = in d e x ( z ) S x ′ = { i n d e x ( z ) : z ∈ S x } S_x^{^{\prime}}=\{index(z):z\in S_x\} S x ′ = { in d e x ( z ) : z ∈ S x }
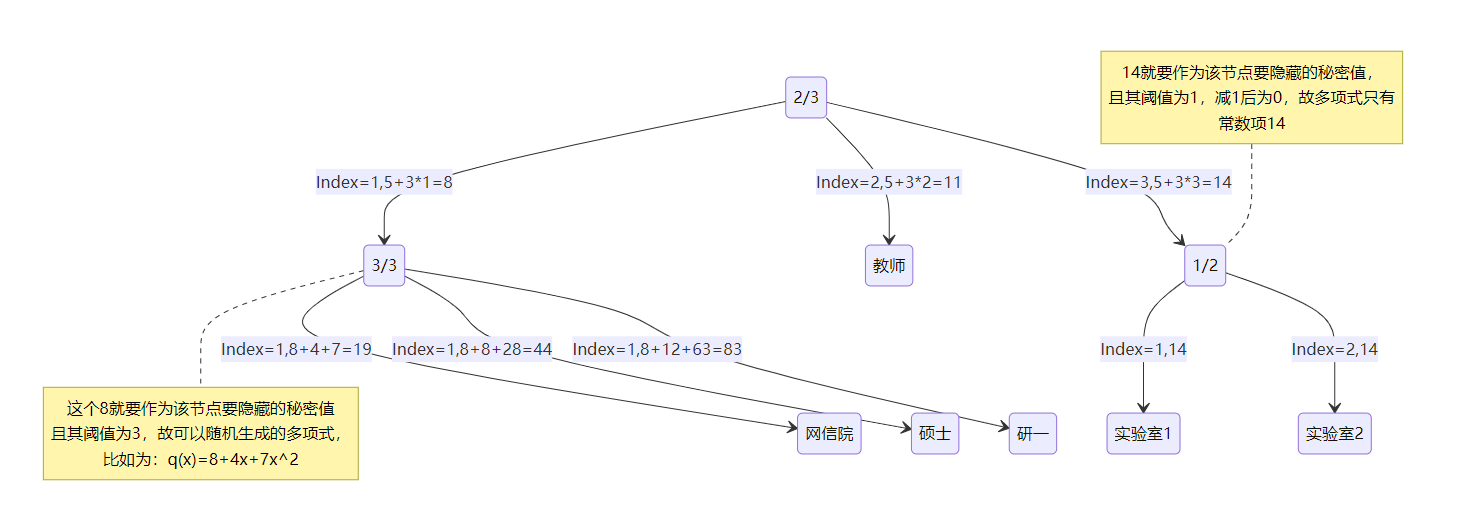
结合上面的例子,我们现在有"计算机学院"(1,19)、“硕士”(2,44)和"研一"(3,83),所以,根据拉格朗日插值法,我们可以算出这三个节点的父节点的多项式是q x ( x ) = 8 + 4 x + 7 x 2 q_x(x)=8+4x+7x^2 q x ( x ) = 8 + 4 x + 7 x 2 q R ( x ) = 5 + 3 x q_R(x)=5+3x q R ( x ) = 5 + 3 x