1.访问控制加密（ACE）

首先先弄清楚啥是ACE（Access Control Encryption）。

以前Bell和LaPadul[1]

提出了IFC（information flow control）的概念，它可以限制系统中，谁可以接收消息以及谁可以发送消息，但是我们还需要更多功能，比如限制谁可以写密文并传输，由此， Damg ̊ard等人[2]提出了ACE。

  • ACE方案中定义了两个安全概念：No-READ rule和No-WRITE rule。未授权的接收者不能解密密文、未授权的发送者不能发送消息。

  • ACE 方案假定所有通信都通过一个诚实但好奇的第三方（称为 Sanitizer）进行传输。诚实且好奇指sanitizer遵守协议规范，但可能会尝试推断一些敏感信息，包括用户（发送方和接收方）的身份或者破坏消息的机密性。会在传输消息之前，在不知道消息新内容和用户身份的情况下，对消息进行一些操作。

2.与门访问结构（AND-gate）

与门访问结构属于单调访问结构的一种。啥是单调访问结构呢？

令P={P1,P2,...,Pn}P=\left\{P_{1},P_{2},...,P_{n}\right\}为一系列参与者的集合，令其幂集为

2P=2{P1,P2,...,Pn}={A∣A⊆{P1,P2,...,Pn}}2^{P}=2^{\{P_{1},P_{2},...,P_{n}\}}=\{A|A\subseteq\{P_{1},P_{2},...,P_{n}\}\}

集合A⊆2PA\subseteq 2^P是单调的，当且仅当任意子集B,C∈PB,C\in P，如果B∈AB\in A且B⊆CB\subseteq C，则C∈AC\in A。一个访问结构（单调访问结构）是P1,P2,…,Pn{P_1,P_2,\dots,P_n}的幂集的非空子集，即A⊆2P∖{∅}A\subseteq2^P\setminus\{\emptyset\}，在AA中的集合为授权集合，不在AA的集合为非授权集合。

解释：AA是参与者集的幂集的子集，是一个集合的集合，B,CB,C是参与者集的子集, 当BB包含于AA时，即是AA中一个元素(集合)时，若同时BB是CC的子集, 使得CC也包含于AA，即CC也是AA的一个元素(集合)，则AA是单调的。直观上理解就是AA中的元素(集合)，所包含的参与者集是单调增长的，Venn图画出来大致就是这样，一个集合包含一个集合，没有偏离的部分。

image-20231110171725039

举例：假设有用户{1,2,3,4},只有 (1,2) 合作，或者 (3,4) 合作可以恢复秘密，(1,3,4) 当然也可以恢复秘密，但是 (1,3,4) 不是 ((1,2),(3,4)) 的超集。

注: CP-ABE中，属性就是参与者，所以满足密文访问结构的属性集合，就是定义的授权集。通常只考虑单调访问结构。

与门访问结构又可以细分为普通与门，支持正负属性的与门、支持正负属性和通配符的与门、支持多值属性的与门、支持多值属性和通配符的与门。由于支持多值属性和通配符的与门访问结构相对其他的与门访问结构更加灵活，且可以实现密文的长度恒定，具有良好的特性，所以这里只介绍这种访问结构[3]

假设U={att1,att2,…,attn}U=\{att_1,att_2,\ldots,att_n\}表示系统所有属性的集合，同时每一个属性attiatt_i能够拥有多个属性值Si={vi,1,vi,2,…,vi,ni}S_i=\{v_{i,1},v_{i,2},\ldots,v_{i,n_i}\}，令ni=∣Si∣n_i=|S_i|，表示SiS_i的个数。假设用户具有的属性集为L=[L1,L2,…,Ln]L=[L_1,L_2,\ldots,L_n]，并且访问结构为W=[W1,…,Wn]=Λi∈IWWiW=[W_1,\ldots,W_n]=\Lambda_{i\in I_W}W_i，其中IWI_W是下标索引集合IW={i∣1≤i≤n,Wi≠∗}I_W=\{i|1\leq i\leq n,W_i\neq*\}，上面的访问结构其实就是所有元素Wi∼WnW_i\sim W_n的交集。用户属性集的某个属性值LiL_i和访问结构中的元素值WiW_i是一一对应的，如果对于1≤i≤n1\leq i\leq n的ii，若Li=WiL_i=W_i或 Wi=∗W_i=*，那么LL就满足WW；否则LL不满足WW，其中∗*可以表示任何值。

举例：如下图，访问结构中n=5n=5，访问结构逻辑表达式为W=[A2,B1,C∗,D4,E2]W=[A2,B1,C*,D4,E2]。假设系统用户Alice的属性列表为LAlice=[A2,B1,C1,D4,E2]L_{Alice}=[A2,B1,C1,D4,E2]，Bob的属性列表LBob=[A1,B2,C1,D4,E2]L_{Bob}=[A1,B2,C1,D4,E2]。由此可知，Alice满足而Bob不满足。

flowchart TD
	and((AND))---A2
    and((AND))---B1
    and((AND))---C*
    and((AND))---D4
    and((AND))---E2

3.双线性对映射

3.1 群

群就是一些元素和这些元素的运算方式（可以是加减乘除）的集合，但这些元素里有一个很特殊的，就是单位元，单位元和这些元素里除了单位元之外的元素运算后，还是那个元素。比如整数集里面，加法的单位元就是0；乘法的单位元则是1。单位元通常用ee来表示。

3.2 循环群

设群<G,∙><G,\bullet>，其中∙\bullet表示群里的运算方式，在这个群里如果存在一个元素gg，即g∈Gg\in G，使得GG中的每个元素都可以用gig^i的形式表示（ii为整数），那么就称<G,∙><G,\bullet>是一个循环群，那么这个gg就是这个群的生成元。如果∙\bullet表示乘法，那么就称这个循环群为乘法循环群。

综上，群里的每个元素都是生成元gg通过ii次自运算得到的。比如乘法循环群，gi=g⋅g…⋅g⏟ig^i=\underbrace{g\cdot g\ldots\cdot g}_i

3.3 阶

设群<G,∙><G,\bullet>，使得ak=ea^k=e成立，kk为正整数，kk可有多个，在kk的所有取值中，找到最小的那个正整数当作这个群的阶。

我先认为ak=ea^k=e成立，那么a2k=ak⋅ak=e⋅e=ea^{2k}=a^k \cdot a^k=e \cdot e=e，那么ank=ak…ak⏟n=e…e⏟n=ea^{nk}=\underbrace{a^k\ldots a^k}_n=\underbrace{e\ldots e}_n=e，所以kk可以是nknk（nn为正整数），在一个含有无数个元素的循环群里，kk也有无数种可能，但在有限个元素的循环群中，我们就取所有可能值中最小的那个。

这时就可以得出一个循环群里的所有元素都可以通过生成元gg的自运算得到，然后它自运算kk次后就得到了群的单位元，而且gg自运算的次数在1到kk之间的每次变化就会得到不同的群元素，那么gg自运算的次数达到kk次时，得到群的单位元，自运算到2k2k时，又得到单位元。那么自运算次数从1到kk的结果是否与自运算次数k+1k+1到2k2k的结果相同呢？

假设生成元为gg，阶数为kk，自运算次数从1到kk，那么得到的群元素为g1,g2,…,gk=eg^1,g^2,\ldots,g^k=e；自运算次数从k+1k+1到2k2k，易得gk+1=gk⋅g=e⋅g=g,gk+2=gk⋅g2=e⋅g2=g2,…,g2k=gk⋅gk=e⋅e=e\begin{aligned}&g^{k+1}=g^k\cdot g=e\cdot g=g,g^{k+2}=g^k\cdot g^2=e\cdot g^2=g^2,\ldots,g^{2k}=g^k\cdot g^k=e\cdot e=e\end{aligned}，发现结果是一一对应的。由此，阶数kk就是一个循环周期的长度。

还有个问题，为什么gk=eg^k=e？生成元自运算了阶数kk次就正好得到单位元ee？这里引出一个限制条件，生成元在一个循环周期kk内进行相应的自运算次数后，它要有kk个不能重复的元素。

现在拿一个模6的加法循环群来举例，它的元素有0，1，2，3，4，5，其中0是单位元。下表横轴表示运算次数，模6的结果就是除以6后取的余数。

元素 1 2 3 4 5 6
0 0 0 0 0 0 0
1 1 2 3 4 5 0
2 2 4 0 2 4 0
3 3 0 3 0 3 0
4 4 2 0 4 2 0
5 5 4 3 2 1 0

由表可知，每个元素都有它对应的阶，例如2的循环周期是3，即一组（2，4，0）为一个周期。能生成完整群元素的只有元素1和5，而元素2，3，4的周期只能生成部分元素，进一步，元素1和5与6互素，元素2，3，4对应的阶数是群阶数6的公因子。那么，当元素与群阶数互素时，元素阶数就是最大公因子，也就是群阶数。

综上，选择生成元时，要选择与群阶数互素的元素来作为生成元。

综上，基于生成元得到的群阶数为群里不重复元素的最大个数。

3.4 双线性对映射

设GG和G1G_1分别是阶为素数pp的乘法循环群，gg为GG的生成元。若映射e:G×G→G1e:G\times G\to G_1能满足以下条件，则称ee为双线性对映射：

  • 双线性性：∀u,v∈G\forall u,v\in G和∀a,b∈Zp∗\forall a,b\in Z_p^*，都满足e(ua,vb)=e(u,v)abe(u^a,v^b)=e(u,v)^{ab}；
  • 非退化性：∃u,v∈G\exists u,v\in G，使得e(u,v)≠1e(u,v)\neq1，其中1是GG的单位元；
  • 可计算性：∀u,v∈G\forall u,v\in G，存在有效算法能计算e(u,v)∈G1e(u,v)\in G_1。

双线性对映射具有如下性质：

  • ∀u1,u2∈G\forall u_1,u_2\in G，有e(u1u2,v)=e(u1,v)e(u2,v)e(u_1u_2,v)=e(u_1,v)e(u_2,v)；
  • ∀u,v∈G,∀a,b∈Zp∗\forall u,v\in G,\forall a,b\in Z_p^*，有e(ua,vb)=e(u,v)ab=e(ub,va)e(u^a,v^b)=e(u,v)^{ab}=e(u^b,v^a)。

映射ee本质上就相当于函数运算一样，我们有两个输入，然后经过映射ee的函数运算之后得到一个结果。这个结果是属于G1G_1的。然后满足上面那三个条件了，我们就称其为双线性映射。其实，我们理解到这里就行了，重要的是利用它的性质来计算。

4.拉格朗日插值法

这里引用一下这篇文章的例子[4]

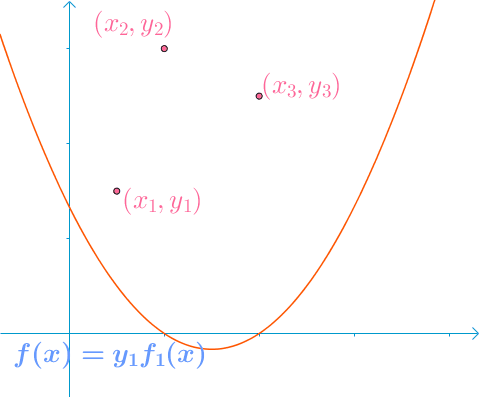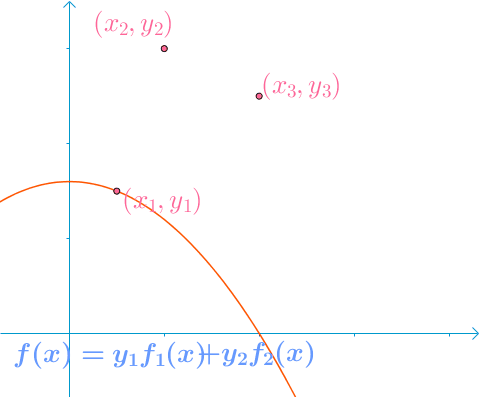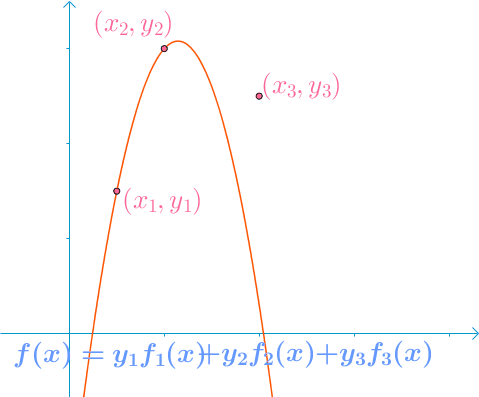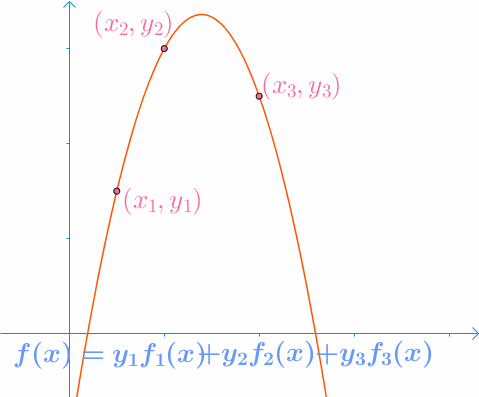
1821690-20211113201725228-1496070439

假设我们的秘密值是S=1234S=1234，我们希望将秘密分为6个部分（n=6n=6），其中3个部分的任何子集k=3k=3足以重建秘密值。

我们随机获得2个数字：166，94（a1=166，a2=94a_1=166，a_2=94），由此用于产生秘密份额（点）的多项式为：

f(x)=1234+166x+94x2f(x)=1234+166x+94x^2

从该多项式构造6个点：（1，1494）（2，1942）（3，2578）（4，3402）（5，4414）（6，5614），我们给每个参与者一个不同的单点（xx和f(x)f(x)）。

为了重建秘密，任何3份就够了。考虑（2，1942）（4，3402）（5，4414）三点，通过下式计算

Li(x):=∏j≠itx−xj′xi′−xj′∈Zq[x]fori=1,…,tL_i(x):=\prod\limits_{j\neq i}^t\frac{x-x_j^{\prime}}{x_i^{\prime}-x_j^{\prime}}\in\mathbb{Z}_q[x]\quad\mathrm{for} \quad i=1,\ldots,t

ℓ0=x−x1x0−x1⋅x−x2x0−x2=x−42−4⋅x−52−5=16x2−112x+313ℓ1=x−x0x1−x0⋅x−x2x1−x2=x−24−2⋅x−54−5=−12x2+312x−5ℓ2=x−x0x2−x0⋅x−x1x2−x1=x−25−2⋅x−45−4=13x2−2x+223\begin{aligned}\ell_0&=\frac{x-x_1}{x_0-x_1}\cdot\frac{x-x_2}{x_0-x_2}=\frac{x-4}{2-4}\cdot\frac{x-5}{2-5}=\frac16x^2-1\frac12x+3\frac13\\\ell_1&=\frac{x-x_0}{x_1-x_0}\cdot\frac{x-x_2}{x_1-x_2}=\frac{x-2}{4-2}\cdot\frac{x-5}{4-5}=-\frac12x^2+3\frac12x-5\\\ell_2&=\frac{x-x_0}{x_2-x_0}\cdot\frac{x-x_1}{x_2-x_1}=\frac{x-2}{5-2}\cdot\frac{x-4}{5-4}=\frac13x^2-2x+2\frac23\end{aligned}

由此

f(x)=∑j=02yj⋅ℓj(x)=1942⋅(16x2−112x+313)+3402⋅(−12x2+312x−5)+4414⋅(13x2−2x+223)=1234+166x+94x2\begin{aligned} &f(x)=\sum_{j=0}^2y_j\cdot\ell_j(x) \\ &=1942\cdot\left(\frac16x^2-1\frac12x+3\frac13\right)+3402\cdot\left(-\frac12x^2+3\frac12x-5\right)+4414\cdot\left(\frac13x^2-2x+2\frac23\right) \\ &=1234+166x+94x^2 \end{aligned}

通过上图这样的计算，只要满足了设定的单点个数，就能恢复出原始的秘密值。比如现在有个访问策略有6个属性，只要满足其中3个就可以恢复出秘密值，这就扩展了访问策略的复杂性，使其支持更多场景下的访问策略的设定。

5.二进制表示集合中的子集（Binary Representation of a subset）

对于一个给定的宇集合UU（大小为nn），可以使用长度为nn的二进制字符串来表示集合UU的每个子集。这种表示方法通常用于在计算机科学和离散数学中处理集合和子集的问题。

在这种表示法中，二进制字符串的每一位对应于集合 U 中的一个元素。如果某个元素属于子集AA，则对应的二进制位就设为 1；如果不属于子集AA，则设为0。这样，通过检查二进制字符串的每一位，就可以确定集合中的元素是否包含在子集中。

例如，如果集合U={a,b,c}U = \{a, b, c\}，而子集A={a,c}A = \{a, c\}，那么它的二进制表示可以是 (1, 0, 1)。这里，第一位对应于元素 a，设为 1 表示 a 在子集中；第二位对应于元素 b，设为 0 表示 b 不在子集中；第三位对应于元素 c，设为 1 表示 c 在子集中。

  1. 1.D Elliott Bell and Leonard J LaPadula. Secure computer systems: Mathematical foundations. Technical report, DTIC document, 1973. ↩
  2. 2.Ivan Damg˚ard, Helene Haagh, and Claudio Orlandi. Access control encryption: Enforcing information flow with cryptography. In Martin Hirt and Adam D. Smith,editors, TCC 2016-B, Part II, volume 9986 of LNCS, pages 547–576. Springer,Heidelberg, October / November 2016. ↩
  3. 3.Ling Cheung and Calvin Newport. 2007. Provably secure ciphertext policy ABE. In Proceedings of the 14th ACM conference on Computer and communications security (CCS '07). Association for Computing Machinery, New York, NY, USA, 456–465. https://doi.org/10.1145/1315245.1315302 ↩ ↩
  4. 4.https://zhuanlan.zhihu.com/p/386078331 ↩